Estimating Our Tricks E(tricks) = trumps + (HCP-20)/3 + e
#1

Posted 2013-June-24, 16:02
Nearly all systems evaluate a hand from the viewpoint of one player and in terms of points. These points are usually high card points with adjustments for shortness in the side suits or additional points for length. It is time for players to attempt to assess the value of his hand in terms of playing tricks for the partnership. This assessment is a dynamic number which changes during the auction as the location of more of the other 39 cards is revealed. The estimate of our playing tricks is dynamic, keeps changing as more information is available. It is not static. This estimate is not a number written in stone.
Before one removes his cards from the tray, the expected tricks is 6 1/2. We expect to win half of the available 13 tricks. Remove the cards and sort the hand. Tally our points. The estimate of our expected tricks is not a single value. It is a set of values depending on the strain of the final contract. With each board there are five evaluation models: one for notrumps and one each for each of the four suits. This estimate also has a margin of error depending on the location of all 52 cards. The standard deviation of the error of our initial estimate is nearly 3 tricks. When we know the strain and the combined partnership HCP the std dev drops to 1.5 to 2 tricks. When we also know the sum of our combined trumps the std dev drops even further to 1 to 1.25 tricks.
The estimate of our tricks for the general case.
E(tricks) = trumps + (HCP-20)/3 + e
Trumps is the total combined trumps of the partnership.
(HCP-20)/3 means for every HCP over 20 assign another 1/3 trick to the estimate.
The curve generated by this equation is approximated by the normal curve(bell curve).
'e' is the error of the observations. E(e)=0.
For large samples the average error will approach zero.
The third parameter for estimating tricks is flatness/skewness. Lawrence/Wirgren uses short suit totals(SST). With sufficient trumps well placed singletons and voids can be worth additional tricks. Additional length in the side suit can also produce extra tricks. Every new parameter adds another term to the equation for estimating tricks. The more independent variables in our model the smaller the variance of our estimates. Smaller variance means better estimates.
jogs
#2

Posted 2013-June-24, 18:19
E(tricks) = [trumps + (hcp-20)]/3.
Otherwise you have the patently absurd proposition that Jxxxx opposite xxxxx always plays for 10 tricks.
Bear in mind that the revised formula is absurd as well. Jxxxxxxxxx opposite void will always play for at least 7 tricks even with no other hcp in the combined hands.
I recognize that you suggest other parameters, and obviously you'd need to adjust for shape in some manner.
However, the more serious complaint is that we appear to be seeing the nth effort to reduce the multi-factorial, and subtle, process of hand evaluation to some sort of algorithmic approach using only a handful of factors.
Expert players, imo, use many factors, and much of the valuation process is subconscious. All players claiming to be advanced or better already know that hand evaluation is an ongoing process throughout the auction. Heck even Culbertson, in the 1930s, cautioned his readers that hand valuation was constantly changing during the bidding.
There may be at the end of the day a possibility that one could craft an arithmetical approach that would emulate or even outdo the best humans, but such an approach will be very complex and I doubt that any human would ever be able to implement it at the table, partly because the conscious calculation process would likely be beyond human abilities to complete in timely fashion and partly because the gain would likely be marginal compared to the cost.
In the meantime, attempts to reduce this game to over-simplified metrics arguably serve to impair one's ability to actually get better at bidding by developing those subtle and unconsciously learned and applied methods that end up being called: judgment.
#3

Posted 2013-June-25, 07:27
This is least square estimates. This is analysis of variance.
For individual observations it is
y = trumps + (HCP-20)/3 + e
For better estimates
y = A+B + (HCP-20)/3 + e
where A is my trumps and B is pard's trumps.
4+4=8 trumps does not generate the exact same distribution
as 5+3=8 trumps.
The 'e' for error is standard for statistics. This 'e' accounts
for variation of the results. Its the fudge factor. It acknowledges
that many other parameters influencing the results were not
included in our model.
#4

Posted 2013-June-26, 04:46
but do you have evidence that the factor 1/3 is accurate?
I made a regression analysis for suit contracts, similar idea but more complex since I allowed for the values of the honors to depend on the suit length:
http://www.bridgebas...s-investigated/
#5

Posted 2013-June-26, 18:53
 helene_t, on 2013-June-26, 04:46, said:
helene_t, on 2013-June-26, 04:46, said:
but do you have evidence that the factor 1/3 is accurate?
It's an estimate. A king equal 3 points and is worth approximately a trick.
Therefore a point is approximately 1/3 of a trick.
Have run studies on 4-4 fits and 5-4 fits. The std dev for the results
is around 1.25 tricks/board.
When short suit totals is included in the model, the std dev is about
1 tricks/board on flat hands. Flat hands depresses tricks. Even in
the general case it can be as much as one full trick less. In specific
boards it sometimes can be as many as three tricks less.
5=3=3=2 facing 4=3=3=3. This pattern pair reduces tricks.
5=3=3=2 facing 5=3=2=3. If we have only 20 HCP, expect to make
only nine tricks. When partner opens 1M(5-card majors), don't
jump to 4M. The LAW does not protect you.
#6

Posted 2013-June-28, 16:47
Quote
Ace=1.5 (but 1 if stiff)
King=1 (but zero if stiff)
Q=0.5 (zero if stiff or if in doubleton)
♠AT987 ♥A765 ♦A42 ♣A
Should be obvious the aces in spades, hearts, and diamonds are worth
different values.
I don't like double dummy analysis. Prefer viewing results from live play.
K facing xxx in 3NT. Sometimes the opening leader with AJ752 leads
fourth best. The king steals a trick. Other times partner holds Axx or
Qxx.
Queens generally have no value unless supported by aces and kings.
AQ facing xx. That's worth 1 1/2 tricks.
Qxx facing xxx. Worth zero tricks.
Qxx facing Jxx. Worth one trick only when opponents cooperate.
Quote
Singleton=2
Doubleton=1
These numbers aren't tricks. They are loser points.
Doesn't everyone play with a 4-4 fit in a major and 25 HCP bid
game? The expected tricks is 9 2/3. Expect to make this game
45+% of the time. But it's really
E(tricks) = 9 2/3 +/- 1.25 tricks.
Sometimes we go down. Still next time we bid game again.
We are working with statistical probability. No system will be
right all the time. We are just hoping to be right more often
than the other guy.
.............................
Just read Terry S. Feetham's article from The Bridge World August
2006.
Not familiar with Feetham's statistical methodology. It is normal
to test the estimate from a model against each observed result
separately. Then report the average error and standard deviation
of that error. Feetham compared his estimate from his model with
the average of the observed results. Those are two different
methods.
#7

Posted 2013-July-01, 02:33
#8

Posted 2013-July-01, 03:27
 Zelandakh, on 2013-July-01, 02:33, said:
Zelandakh, on 2013-July-01, 02:33, said:
My database is not set up that way - it is basically a text/pbn file where I can search for any auction.
I was thinking of making a second version using the methods Ben suggested to make an Excel version, but it may be beyond me.
#9

Posted 2013-July-01, 09:05
 Zelandakh, on 2013-July-01, 02:33, said:
Zelandakh, on 2013-July-01, 02:33, said:
I could try that but it wouldn't be that many hands.
#10

Posted 2013-July-01, 09:36
 PhilKing, on 2013-July-01, 03:27, said:
PhilKing, on 2013-July-01, 03:27, said:
I was thinking of making a second version using the methods Ben suggested to make an Excel version, but it may be beyond me.
It may take a day or two. I will post how to calculate standard deviation on Excel.
The simple lo...ng way is to post every observation on a separate line.
Have separate columns for expected tricks(by model), observed tricks, and first differences.
Then find the variance of the first differences.
Click the fx icon.
Click 'statistical' under function category.
Scroll down on function name and click 'VAR'.
The std dev is the square root of the variance.
Will post the other way later. Requires a few subroutines.
#11

Posted 2013-July-01, 09:44
 Zelandakh, on 2013-July-01, 02:33, said:
Zelandakh, on 2013-July-01, 02:33, said:
The 4-4 major fit with 25 points might not be the best way to test this equation. Better is to look at a huge series of suit contracts show the degree of fit and the point count and compare with the double dummy number of tricks. But MikeH's concerns in his post remain. Look at, for instance the equation.
For better estimates
y = A+B+(HCP20)/3 + e
where A is my trumps and B is pard's trumps
e is some "fudge factor", for the sake of argument, lets call it 0 (that is, we will not add anything to our number of tricks.. Then take this pair of hands.
Jxxxx
xx
xxx
xxx
Txxxx
xx
xxx
xxx
The values in this would be...
y = 5 + 5 + 1/3 + 0 = 10.3 tricks
How many tricks do you think these two hands take? I would say between 2 and 3 tricks, quite a difference from the number estimated by the equation even without adding back anything for "e". Make a small change to the hand, and exchange hearts and diamond in south, an you gain a trick (3 to 4). Move all three of south's clubs to diamonds, and it will take at least two more tricks (4 to 5) all without changing the equation or the values in it.
I ran a quick simulation like you asked for using deal masterpro. Only constrain anywhere was the NS had a 4-4 major fit and a combined 25 HCP. They could have any other distribution as could the opponents. I only did 100 hands because I don't think this is the best way to test this equation. The number of tricks NS could win were (out of 100)
8 -- 6 times
9 -- 18 times
10 -- 36 times
11 -- 34 times
12 -- 5 times
13 -- 1 time
#12

Posted 2013-July-01, 10:01
Number of tricks taken:
7: 1 time
8: 7 times
9: 22 times
10: 44 times
11: 20 times
12: 6 times
13: 0 times
#13

Posted 2013-July-01, 11:11
So the equation needs to modified as suggest by MikeH and ignored by Jogs...
Y = (A +B + pts)/3 = (8 + 8.33)/3 = 16.33/3 = 5.44 so that doesn't work either.. Maybe e is five?
#14

Posted 2013-July-01, 12:59
trump is worth 0.5 additional tricks. The tenth trump is worth
0.5 additional tricks.
Disagree with Feetham.
I posted.
Quote
E(tricks) = trumps + (HCP-20)/3 + e
Trumps is the total combined trumps of the partnership.
(HCP-20)/3 means for every HCP over 20 assign another 1/3 trick to the estimate.
The curve generated by this equation is approximated by the normal curve(bell curve).
'e' is the error of the observations. E(e)=0.
For large samples the average error will approach zero.
Confession. It ain't necessarily so. This model starts to break down at
the four level. Controls which play a secondary role in low level contracts
are a primary parameter in high level contracts.
When trumps equal 8 or 9 the expected value of the error is
nearly zero. The ninth trump is worth one full additional trick.
When trumps >= 10 , E(e)<0.
That means when we have 20 HCP and 10 trumps, our expected tricks
is less than 10. The tenth trump does not produce a full additional
trick. It is more than 0.5 and less than 1 trick. From the tenth trump
on each successive trump is worth fewer fractional tricks than the
previous trump.
It should be obvious that with 20 HCP and 13 trumps, our expected
tricks is less than 13. Only need to find one example where tricks
are less than 13. Will never find a board producing 14+ tricks.
This also means in LoTT expected tricks equal total trumps is only
true when total trumps is 18 or less. When total trumps is equal or
greater than 19, the expected tricks is less than the total trumps.
#15

Posted 2013-July-01, 13:06
 inquiry, on 2013-July-01, 11:11, said:
inquiry, on 2013-July-01, 11:11, said:
So the equation needs to modified as suggest by MikeH and ignored by Jogs...
Y = (A +B + pts)/3 = (8 + 8.33)/3 = 16.33/3 = 5.44 so that doesn't work either.. Maybe e is five?
Ignored because MikeH is clearly wrong. He thinks an additional trump
is worth no more than an additional point.
A trump is worth approximately one extra trick.
A king is worth approximately one extra trick.
A king is worth approximately 3 points.
A trump is worth approximately 3 points.
But all this breaks down once the estimates are 10 or more tricks.
Other parameters not included in the model start playing a larger
role on the estimates of tricks.
#16

Posted 2013-July-01, 15:49
 jogs, on 2013-June-25, 07:27, said:
jogs, on 2013-June-25, 07:27, said:
This is least square estimates. This is analysis of variance.
For individual observations it is
y = trumps + (HCP-20)/3 + e
For better estimates
y = A+B+(HCP20)/3 + e
where A is my trumps and B is pard's trumps.
4+4=8 trumps does not generate the exact same distribution
as 5+3=8 trumps.
The 'e' for error is standard for statistics. This 'e' accounts
for variation of the results. Its the fudge factor. It acknowledges
that many other parameters influencing the results were not
included in our model.
Sorry, lost a minus sign. Should read
y = A+B+(HCP-20)/3 + e
#17

Posted 2013-July-02, 01:08
E(y) = T1 + T2 + (MH - 26)/4,
where T1 = number of trumps in Declarer's hand
and T2 = number of trumps in Dummy
and MH = modified hcp (A = 6, K = 4, Q = 2, J = 1)
See if that improves your estimate for >= 10 tricks.
#18

Posted 2013-July-04, 14:08
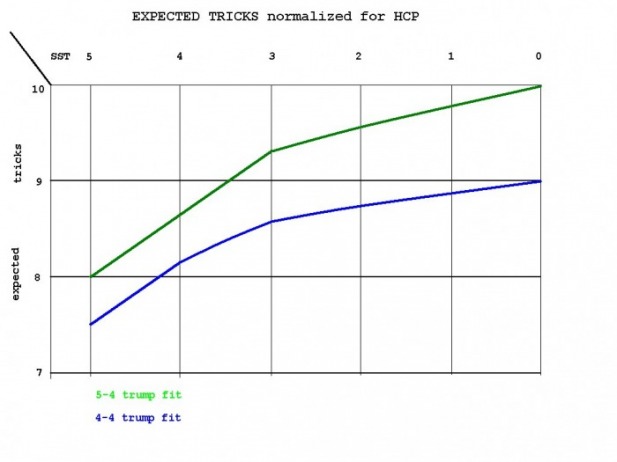
Normalized here means each side holds 20 points.
#19

Posted 2013-July-04, 14:12
been posting this model on RGB for over 3 years.
Since the beginnings of bridge most bidding systems were based
on pointcount with modifications. Those bidding systems ignored
the effects of trumps on tricks. Ignored how tricks fluctuate wildly
depending on strain.
Larry Cohen used Jean-René Vernes' discovery of the relationship
between trumps and tricks to develop his total tricks model.
This model combines both points and trumps to estimate tricks.
This method accounts for fluctuations due to strain.
E(tricks) = trumps + (HCP-20)/3 + e
This model's reliability starts to break down on the four level.
Lawrence/Wirgren discovered that skewness/flatness also affects
tricks. In the general case flatness can reduce the estimates by
one full trick. Skewness can increase the estimates by one full
trick. The main drawback is one doesn't often know his partner's
exact pattern. We do know when our own hand is flat tricks are
reduced.
Flat hands reduce expected tricks. 4333, 4432, 5332, and 5422
generates fewer tricks than the two random variable model would
suggest. Even 6322 and 7222 often disappoint.
E(tricks) = trumps + (HCP-20)/3 + SF + e
In the general case the SF term should range from -1 to +1.
The affects of SF is measured for the normalized 4-4 fit and
the normalized 5-4 fit. Chart is posted on previous post #18.
#20

Posted 2013-July-04, 14:16
 Zelandakh, on 2013-July-02, 01:08, said:
Zelandakh, on 2013-July-02, 01:08, said:
E(y) = T1 + T2 + (MH - 26)/4,
where T1 = number of trumps in Declarer's hand
and T2 = number of trumps in Dummy
and MH = modified hcp (A = 6, K = 4, Q = 2, J = 1)
See if that improves your estimate for >= 10 tricks.
Already explained that from the combined tenth trump on,
each successive trump is worth fewer fractional tricks
than the previous trump. Also controls play a larger
role on tricks in high level contracts.

 Help
Help

